1. 经典策略
  2. 多因子选股(股票)
PDF下载 下载
“”关键字 0 个。
2/10

多因子选股(股票)

阅读 171096

多因子策略

（注：以下部分内容引用自《因子投资：方法与实践》一书）

1. 原理

多因子策略是最广泛应用的策略之一。CAPM模型的提出为股票的收益提供了解释，但随着各种市场异象的出现，使得人们发现股票存在超额收益，这种收益不能为市场因子所解释，因此，出现了多因子模型。

多因子模型最早是由Fama-French提出，包括三因子和五因子模型。Fama认为，股票的超额收益可以由市场因子、市值因子和账面价值比因子共同解释。随着市场的发展，出现许多三因子模型难以解释的现象。因此，Fama又提出了五因子模型，加入了盈利水平、投资水平因子。

此后，陆续出现了六因子模型、八因子模型等，目前多少个因子是合适的尚无定论。

市场上常用的多因子模型包括如下几个。

模型 出处 所含因子
Fama-French三因子 Fama and Farench(1993) 市场、规模、价值
Carhart四因子 Carhart（1997） 市场、规模、价值、动量
Novy-Marx四因子 Novy-Marx（2013） 市场、规模、价值、盈利
Fama-French五因子 Fama and Farench(2015) 市场、规模、价值、盈利、投资
Hou-Xue-Zhang四因子 Hou et al 市场、规模、盈利、投资
Stambaugh-Yuan四因子 Stambaugh and Yuan(2017) 市场、规模、管理、表现
Daniel-Hirshleifer-Sun三因子 Daniel et al（2020） 市场、长周期行为、短周期行为

本策略以Fama提出的三因子模型作为基础。

Fama-French三因子模型

在多因子模型出现以前，CAPM模型被奉为典型，几乎所有定价均是按照CAPM模型计算的。后来学者们发现了各种异象，这些异象无法用CAPM模型解释。较为典型的有Basu发现的盈利市值比效应和Banz发现的小市值效应。遗憾的是，虽然单一异象被发现后都对CAPM提出了挑战，但并没有形成合力，直到Fama三因子模型出现。

Fama等人在CAPM的基础上，Fama加入了HML和SMB两个因子，提出了三因子模型，也是多因子模型的基础。


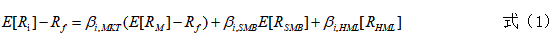
其中E[R_i]代表股票i的预期收益率，R_f代表无风险收益率，E[R_m]为市场组合预期收益率，E[R_SMB]和E[R_HML]分别为规模因子收益率和价值因子预期收益率。

为构建价值因子和规模因子，Fama选择BM和市值两个指标进行双重排序，将股票分为大市值组B和小市值组S；按照账面市值比将股票分为BM高于70%分位数的H组，BM低于30%分位数的L组，BM处于二者之间的记为M组。如表所示。

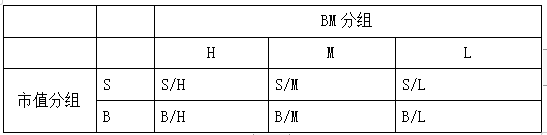
得到上述分组以后，就可以构建规模和价值两个因子。

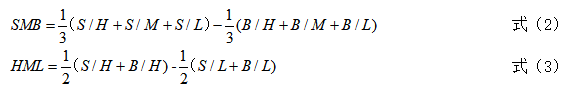
上述式子解释一下可以发现，规模因子是三个小市值组合的等权平均减去三个大市值组合的等权平均；价值因子是两个高BM组合的等权平均减去两个低BM组合的等权平均。

策略设计思路（假设三因子模型是完全有效的）

在用三因子模型估算股票预期收益率时，经常会发现并非每只股票都能严格吻合式1，大部分股票都会存在一个alpha截距项。当存在alpha截距项时，说明股票当前价格偏离均衡价格。基于此，可以设计套利策略。

alpha < 0时，说明股票收益率低于均衡水平，股票价格被低估，应该买入。
alpha > 0时，说明股票收益率高于均衡水平，股票价格被高估，应该卖出。

因此，可以获取alpha最小并且小于0的10只的股票买入开仓。

2. 策略步骤

第一步：获取股票市值以及账面市值比数据。
第二步：将股票按照各个因子进行排序分组，分组方法如上表所示。
第三步：依据式2式3，计算SMB、HML因子。
第四步：因子回归，计算alpha值。获取alpha最小并且小于0的10只的股票买入开仓。

回测期：2017-07-01 8:00:00 至 2017-10-01 16:00:00
回测初始资金：1000万
回测标的：沪深300成分股

3. 策略代码

  1. # coding=utf-8
  2. from __future__ import print_function, absolute_import, unicode_literals
  3. import numpy as np
  4. from gm.api import *
  5. from pandas import DataFrame
  6. '''
  7. 本策略每隔1个月定时触发,根据Fama-French三因子模型对每只股票进行回归，得到其alpha值。
  8. 假设Fama-French三因子模型可以完全解释市场，则alpha为负表明市场低估该股，因此应该买入。
  9. 策略思路：
  10. 计算市场收益率、个股的账面市值比和市值,并对后两个进行了分类,
  11. 根据分类得到的组合分别计算其市值加权收益率、SMB和HML. 
  12. 对各个股票进行回归(假设无风险收益率等于0)得到alpha值.
  13. 选取alpha值小于0并为最小的10只股票进入标的池
  14. 平掉不在标的池的股票并等权买入在标的池的股票
  15. 回测数据:SHSE.000300的成份股
  16. 回测时间:2017-07-01 08:00:00到2017-10-01 16:00:00
  17. '''
  18. def init(context):
  19.     # 每月第一个交易日的09:40 定时执行algo任务（仿真和实盘时不支持该频率）
  20.     schedule(schedule_func=algo, date_rule='1m', time_rule='09:40:00')
  21.     # 数据滑窗
  22.     context.date = 20
  23.     # 设置开仓的最大资金量
  24.     context.ratio = 0.8
  25.     # 账面市值比的大/中/小分类
  26.     context.BM_BIG = 3.0
  27.     context.BM_MID = 2.0
  28.     context.BM_SMA = 1.0
  29.     # 市值大/小分类
  30.     context.MV_BIG = 2.0
  31.     context.MV_SMA = 1.0
  33. # 计算市值加权的收益率的函数,MV为市值的分类对应的组别,BM为账目市值比的分类对应的组别
  34. def market_value_weighted(stocks, MV, BM):
  35.     select = stocks[(stocks['NEGOTIABLEMV'] == MV) & (stocks.['BM'] == BM)] # 选出市值为MV，账目市值比为BM的所有股票数据
  36.     market_value = select['mv'].values     # 对应组的全部市值数据
  37.     mv_total = np.sum(market_value)        # 市值求和
  38.     mv_weighted = [mv / mv_total for mv in market_value]   # 市值加权的权重
  39.     stock_return = select['return'].values
  41.     # 返回市值加权的收益率的和
  42.     return_total = []
  43.     for i in range(len(mv_weighted)):
  44.         return_total.append(mv_weighted[i] * stock_return[i])
  45.     return_total = np.sum(return_total)
  46.     return return_total
  48. def algo(context):
  49.     # 获取上一个交易日的日期
  50.     last_day = get_previous_trading_date(exchange='SHSE', date=context.now)
  51.     # 获取沪深300成份股
  52.     context.stock300 = get_history_constituents(index='SHSE.000300', start_date=last_day,
  53.                                                 end_date=last_day)[0]['constituents'].keys()
  54.     # 获取当天有交易的股票
  55.     not_suspended = get_history_instruments(symbols=context.stock300, start_date=last_day, end_date=last_day)
  56.     not_suspended = [item['symbol'] for item in not_suspended if not item['is_suspended']] 
  57.     fin = get_fundamentals(table='trading_derivative_indicator', symbols=not_suspended,
  58.                            start_date=last_day, end_date=last_day,fields='PB,NEGOTIABLEMV', df=True)  # 获取P/B和市值数据
  60.     # 计算账面市值比,为P/B的倒数
  61.     fin['PB'] = (fin['PB'] ** -1)
  62.     # 计算市值的50%的分位点,用于后面的分类
  63.     size_gate = fin['NEGOTIABLEMV'].quantile(0.50)
  64.     # 计算账面市值比的30%和70%分位点,用于后面的分类
  65.     bm_gate = [fin['PB'].quantile(0.30), fin['PB'].quantile(0.70)]
  66.     fin.index = fin.symbol
  67.     # 设置存放股票收益率的list
  68.     x_return = []
  70.     # 对未停牌的股票进行处理
  71.     for symbol in not_suspended:
  72.         # 计算收益率，存放到x_return里面
  73.         close = history_n(symbol=symbol, frequency='1d', count=context.date + 1, end_time=last_day, fields='close',
  74.                           skip_suspended=True, fill_missing='Last', adjust=ADJUST_PREV, df=True)['close'].values
  75.         stock_return = close[-1] / close[0] - 1
  76.         pb = fin['PB'][symbol]
  77.         market_value = fin['NEGOTIABLEMV'][symbol]
  78.         # 获取[股票代码， 股票收益率, 账面市值比的分类, 市值的分类, 流通市值]
  79.         # 其中账面市值比的分类为：大（3）、中（2）、小（1）
  80.         # 流通市值的分类：大（2）、小（1）
  81.         if pb < bm_gate[0]:
  82.             if market_value < size_gate:
  83.                 label = [symbol, stock_return, context.BM_SMA, context.MV_SMA, market_value]
  84.             else:
  85.                 label = [symbol, stock_return, context.BM_SMA, context.MV_BIG, market_value]
  86.         elif pb < bm_gate[1]:
  87.             if market_value < size_gate:
  88.                 label = [symbol, stock_return, context.BM_MID, context.MV_SMA, market_value]
  89.             else:
  90.                 label = [symbol, stock_return, context.BM_MID, context.MV_BIG, market_value]
  91.         elif market_value < size_gate:
  92.             label = [symbol, stock_return, context.BM_BIG, context.MV_SMA, market_value]
  93.         else:
  94.             label = [symbol, stock_return, context.BM_BIG, context.MV_BIG, market_value]
  95.         if len(x_return) == 0:
  96.             x_return = label
  97.         else:
  98.             x_return = np.vstack([x_return, label])
  100.     # 将股票代码、 股票收益率、 账面市值比的分类、 市值的分类、 流通市值存为数据表
  101.     stocks = DataFrame(data=x_return, columns=['symbol', 'return', 'BM', 'NEGOTIABLEMV', 'mv'])
  102.     stocks.index = stocks.symbol
  103.     columns = ['return', 'BM', 'NEGOTIABLEMV', 'mv']
  104.     for column in columns:
  105.         stocks[column] = stocks[column].astype(np.float64)
  107.     # 计算SMB.HML和市场收益率（市值加权法）
  108.     smb_s = (market_value_weighted(stocks, context.MV_SMA, context.BM_SMA) +
  109.              market_value_weighted(stocks, context.MV_SMA, context.BM_MID) +
  110.              market_value_weighted(stocks, context.MV_SMA, context.BM_BIG)) / 3
  112.     # 获取大市值组合的市值加权组合收益率
  113.     smb_b = (market_value_weighted(stocks, context.MV_BIG, context.BM_SMA) +
  114.              market_value_weighted(stocks, context.MV_BIG, context.BM_MID) +
  115.              market_value_weighted(stocks, context.MV_BIG, context.BM_BIG)) / 3
  116.     smb = smb_s - smb_b
  118.     # 获取大账面市值比组合的市值加权组合收益率
  119.     hml_b = (market_value_weighted(stocks, context.MV_SMA, 3) +
  120.              market_value_weighted(stocks, context.MV_BIG, context.BM_BIG)) / 2
  122.     # 获取小账面市值比组合的市值加权组合收益率
  123.     hml_s = (market_value_weighted(stocks, context.MV_SMA, context.BM_SMA) +
  124.              market_value_weighted(stocks, context.MV_BIG, context.BM_SMA)) / 2
  125.     hml = hml_b - hml_s
  127.     # 获取市场收益率
  128.     close = history_n(symbol='SHSE.000300', frequency='1d', count=context.date + 1,
  129.                       end_time=last_day, fields='close', skip_suspended=True,
  130.                       fill_missing='Last', adjust=ADJUST_PREV, df=True)['close'].values
  131.     market_return = close[-1] / close[0] - 1
  132.     coff_pool = []
  134.     # 对每只股票进行回归获取其alpha值
  135.     for stock in stocks.index:
  136.         x_value = np.array([[market_return], [smb], [hml], [1.0]])
  137.         y_value = np.array([stocks['return'][stock]])
  138.         # OLS估计系数
  139.         coff = np.linalg.lstsq(x_value.T, y_value)[0][3]
  140.         coff_pool.append(coff)
  142.     # 获取alpha最小并且小于0的10只的股票进行操作(若少于10只则全部买入)
  143.     stocks['alpha'] = coff_pool
  144.     stocks = stocks[stocks.alpha < 0].sort_values(by='alpha').head(10)
  145.     symbols_pool = stocks.index.tolist()
  146.     positions = context.account().positions()
  148.     # 平不在标的池的股票
  149.     for position in positions:
  150.         symbol = position['symbol']
  151.         if symbol not in symbols_pool:
  152.             order_target_percent(symbol=symbol, percent=0, order_type=OrderType_Market,
  153.                                  position_side=PositionSide_Long)
  154.             print('市价单平不在标的池的', symbol)
  156.     # 获取股票的权重
  157.     percent = context.ratio / len(symbols_pool)
  159.     # 买在标的池中的股票
  160.     for symbol in symbols_pool:
  161.         order_target_percent(symbol=symbol, percent=percent, order_type=OrderType_Market,
  162.                              position_side=PositionSide_Long)
  163.         print(symbol, '以市价单调多仓到仓位', percent)
  165. if __name__ == '__main__':
  166.     '''
  167.     strategy_id策略ID,由系统生成
  168.     filename文件名,请与本文件名保持一致
  169.     mode实时模式:MODE_LIVE回测模式:MODE_BACKTEST
  170.     token绑定计算机的ID,可在系统设置-密钥管理中生成
  171.     backtest_start_time回测开始时间
  172.     backtest_end_time回测结束时间
  173.     backtest_adjust股票复权方式不复权:ADJUST_NONE前复权:ADJUST_PREV后复权:ADJUST_POST
  174.     backtest_initial_cash回测初始资金
  175.     backtest_commission_ratio回测佣金比例
  176.     backtest_slippage_ratio回测滑点比例
  177.     '''
  178.     run(strategy_id='strategy_id',
  179.         filename='main.py',
  180.         mode=MODE_BACKTEST,
  181.         token='token_id',
  182.         backtest_start_time='2017-07-01 08:00:00',
  183.         backtest_end_time='2017-10-01 16:00:00',
  184.         backtest_adjust=ADJUST_PREV,
  185.         backtest_initial_cash=10000000,
  186.         backtest_commission_ratio=0.0001,
  187.         backtest_slippage_ratio=0.0001)

4. 回测结果与稳健性检验

设定初始资金1000万，手续费率为0.01%，滑点比率为0.01%。回测结果如下图所示。


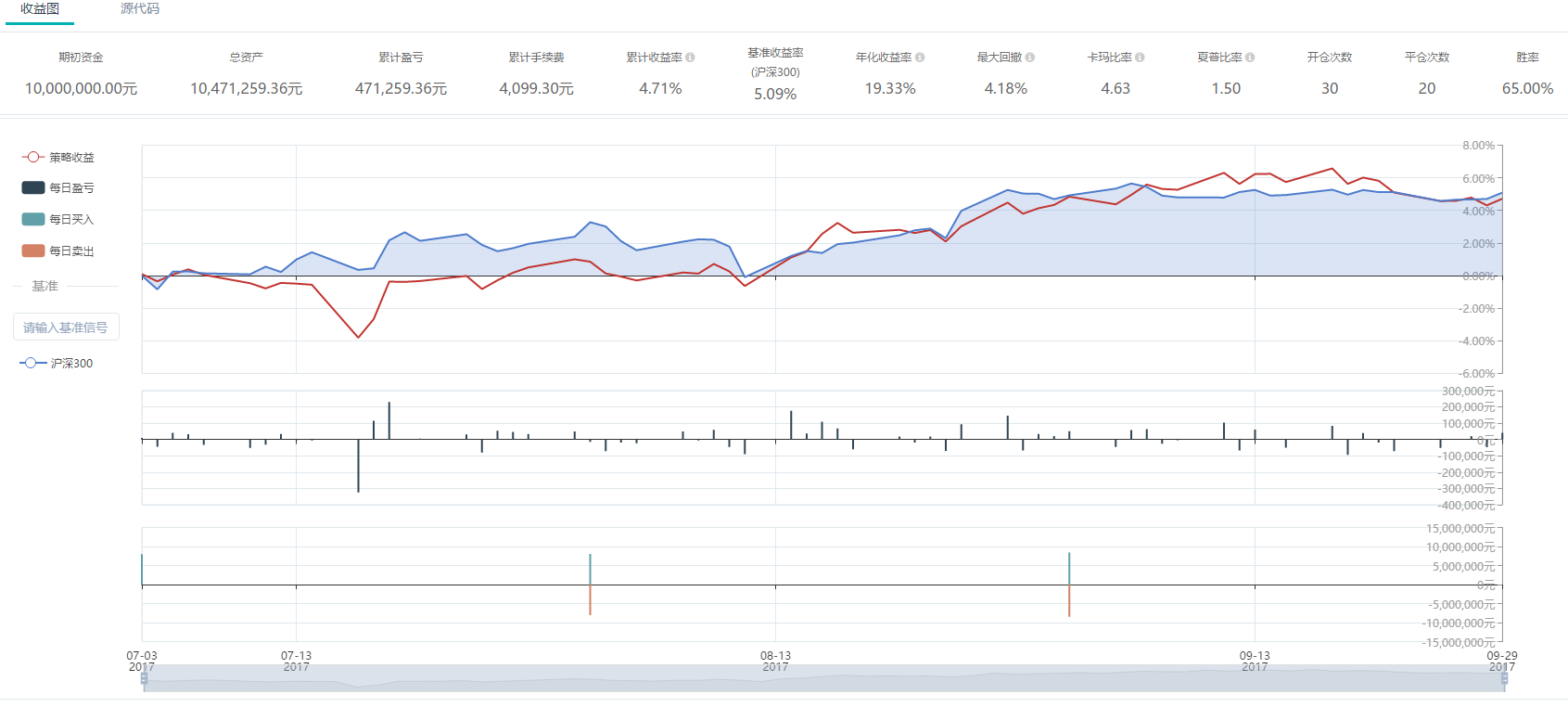
回测期累计收益为4.71%，年化收益率为19.33%，沪深300指数收益率为5.09%，策略整体跑输沪深300指数。最大回撤为4.18%，胜率为65%。

为了检验策略的稳健性，改变回测时间，得到回测结果如下。

回测时间 时间长度 年化收益率 最大回撤
2017.07.01-2017.10.01 3个月 19.33% 4.18%
2017.07.01-2017.12.31 5个月 12.54% 7.53%
2017.07.01-2018.07.01 12个月 -8.09% 23.17%
2017.07.01-2019.07.01 24个月 3.27% 35.38%
2017.07.01-2020.07.01 36个月 6.19% 35.37%

由上表可以看出，策略收益除了在2017年7月1日至2018年7月1日以外其他时间段收益均为正。在2017年7月1日至2017年10月1日期间收益率最高，年化收益率为19.33%。回测期最大回撤随着时间长度的增加而增加，最高达到35.38%，与获得的收益相比，承受风险过大。

注：此策略只用于学习、交流、演示，不构成任何投资建议。

0 篇笔记
分享笔记
联系我们
掘金交流群
掘金交流群
更多群组
微信公众号
微信公众号